Fibonacci

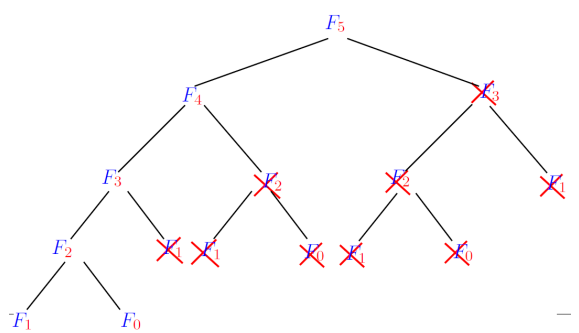
Fibonnaci sequence: each number is the sum of the two preceding ones.

$0,1,1,2,3,5,8,13,21,34,55,89,144,...$

Definition

The fibonacci numbers may be defined by the recurrence relation: $F_0=0,F_1=1,$ $F_n=F_{n-1}+F_{n-2}$

Recursive Algorithm for Fibonacci:

recursive_fibonacci(n):
	if n <= 1
		return n
		else 
			a = recursive_fibonacci(n-1)
			b = recursive_fibonacci(n-2)
			return a + b

number of sums:

Line	Number of sums:
1-2	0
3	T(n-1)
4	T(n-2)
5	1
$T(n)=T(n-1)+T(n-2)+1$

Time consumption is exponential. The algorithm solves the subproblems multiple times.

$T(n)isO(2^n)$

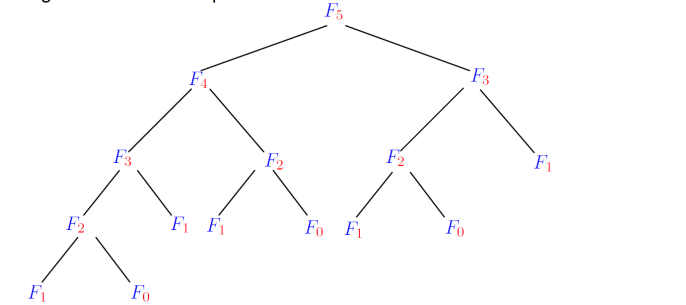
Memoization - Efficiente recursive algorithm

memoized_fibo(f, n):
	for i = 0 to n:
		f[i] = -1
	return lookup_fibo(f,n)

lookup_fibo(f,n):
	if f[n] >= 0
		return f[n];
	if n <= 1
		f[n] = n
	else 
		f[n] = lookup_fibo(f, n-1) + lookup_fibo(f, n-2)
	return f[n];

Time consumption is $\Theta (n)$ The algorithm solves each subproblem only once